函数值域怎么求(函数值域怎么求,公式)

函数值域怎么求

1、通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。例1求函数y=3+√(2-3x)的值域。反函数法 当函数的反函数存在时，则其反函数的定义域就是原函数的值域。例2求函数y=(x+1)/(x+2)的值域。

2、值域的求法 直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。配方法： (或者 说是最值法）求出最大值还有最小值，那么值域就出来了。

3、(1)直接法：从变量x的范围出发，推出y=f(x)的取值范围；(2)配方法：配方法是求“二次函数类”值域的基本方法，形如f(x)=af^(x)+bf(x)+c的函数的值域问题。

4、1．直接法：利用常见函数的值域来求 一次函数y=ax+b(a 0)的定义域为r，值域为r；反比例函数 的定义域为{x|x 0}，值域为{y|y 0}；二次函数 的定义域为r，当a>0时，值域为{ }；当a<0时。

5、直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。配方法：（或者说是最值法）求出最大值还有最小值，那么值域就出来了。

函数的值域怎么求

1、①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和。

2、求值域方法：图像法：根据函数图象，观察最高点和最低点的纵坐标。配方法：利用二次函数的配方法求值域，需注意自变量的取值范围。单调性法：利用二次函数的顶点式或对称轴，再根据单调性来求值域。

3、(1)直接法：从变量x的范围出发，推出y=f(x)的取值范围；(2)配方法：配方法是求“二次函数类”值域的基本方法，形如f(x)=af^(x)+bf(x)+c的函数的值域问题。

4、求值域的五种方法：直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。

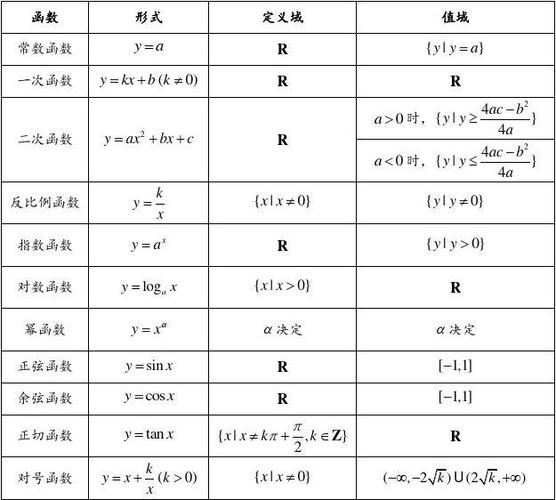
5、常见函数值域：y=kx+b (k≠0)的值域为R y=k/x 的值域为(-∞，0)∪(0，+∞)y=√x的值域为x≥0 y=ax^2+bx+c 当a>0时，值域为 [4ac-b^2/4a，+∞) ；当a<0时，值域为(-∞。

函数的值域的求法

1、直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。配方法：（或者说是最值法）求出最大值还有最小值，那么值域就出来了。

2、函数值域的求法：①配方法：转化为二次函数，利用二次函数的特征来求值；常转化为型如： 的形式；②逆求法（反求法）：通过反解，用 来表示 ，再由 的取值范围，通过解不等式，得出 的取值范围；常用来解。

3、导数法 利用导数求闭区间上函数的值域的一般步骤：(1)求导，令导数为0；(2)确定极值点，求极值；(3)比较端点与极值的大小，确定最大值与最小值即可确定值域。

求值域的五种方法

1、配方法、常数分离、逆求法、换元法、拆分法、单调性法、数形结合法、判别式法。

2、函数值域的求法 配方法：转化为二次函数，利用二次函数的特征来求值；常转化为型如： 的形式；逆求法(反求法)：通过反解，用 来表示 ，再由 的取值范围，通过解不等式，得出 的取值范围；常用来解。

3、⑦单调性法：函数为单调函数，可根据函数的单调性，由定义域求值域。⑧数形结合：根据函数的几何图形，利用数型结合的方法来求值域。

4、求函数值域的常用方法有：配方法，分离常数法，判别式法，反解法，换元法，不等式法，单调性法，函数有界性法，数形结合法，导数法。

函数求值域的17种方法

1、函数的值域可以通过观察法、配方法、常数分离法、换元法、逆求法、基本不等式法、求导法、数形结合法和判别式法等方法来求。配方法 将函数配方成顶点式的格式，再根据函数的定义域，求得函数的值域。

2、高中函数值域的求法：①配方法：化为二次函数，利用二次函数的特征来求值；常转化为型如： 的形式；②逆求法（反求法）：通过反解，用来表示，再由的取值范围，通过解不等式，得出的取值范围；常用来解。

3、求函数值域方法有：1，配方法(二次函数或二次形式的函数求值域的典型方法)2，换元法(比如三角换元，整体代换)3，判别式法 4，利用函数单调性(闭区间上连续函数有最大，最小值)5，数形结合的方法(利用问题的几何意义。

4、函数值域的求法 配方法：转化为二次函数，利用二次函数的特征来求值；常转化为型如： 的形式；逆求法(反求法)：通过反解，用 来表示 ，再由 的取值范围，通过解不等式，得出 的取值范围；常用来解。

函数的值域如何求

1、观察法 通过对解析式的简单变形和观察，利用熟知的基本函数的值域，求出函数的值域。配方法 若函数是二次函数，则可以通过配方并结合二次函数的性质求值域，但要注意给定区间的二次函数最大（小）的求法。

2、值域是函数值所在的集合。一旦函数的定义域和对应法则确定了，函数的值域也就随之确定。

3、函数的值域可以通过观察法、配方法、常数分离法、换元法、逆求法、基本不等式法、求导法、数形结合法和判别式法等方法来求。配方法 将函数配方成顶点式的格式，再根据函数的定义域，求得函数的值域。

4、(1)直接法：从变量x的范围出发，推出y=f(x)的取值范围；(2)配方法：配方法是求“二次函数类”值域的基本方法，形如f(x)=af^(x)+bf(x)+c的函数的值域问题。

5、值域的求法 直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。配方法： (或者 说是最值法）求出最大值还有最小值，那么值域就出来了。